
|
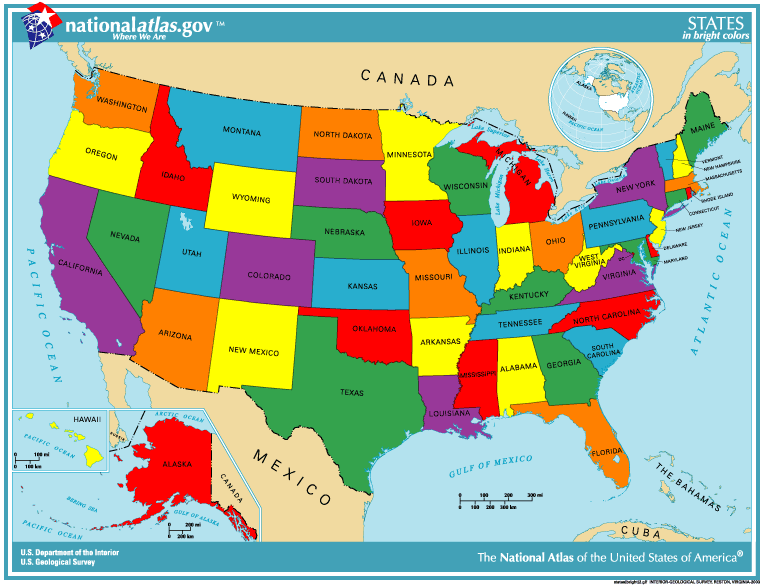
| Colored US map |
| National Atlas |
|
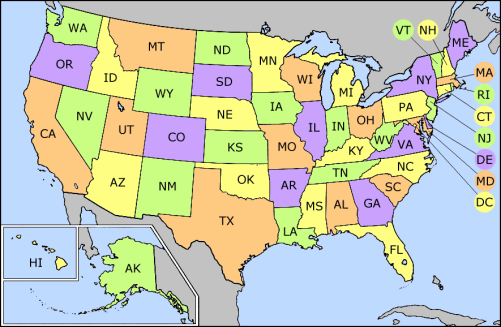
| 4-Colored US map |
| Wikipedia US Map |
The students are first allowed to use any number of colors. Then they are asked if they can use fewer and "What is the smallest number you can use?" The students quickly work it down to 4 colors. (Then they are told about the Four Color Theorem.) Finally, they are asked if it can be done with just 3 colors. If "Yes", do it. If "No", explain why not. (We do not want to give the answer here, because students may read this.)
If the students are running out of time, the map can be cut down to just west or east of the Mississippi. Here is a small map of the Western half of the US.
If they finish, they can be given a blank piece of paper and told to draw 4 lines all the way across the paper, making their own map. They are asked "What is the fewest number of colors that can color this map?" The answer is always 2, (as on a checker board) but the students are asked to explain why. The proof is best done using mathematical induction on the number of lines, but we don't necessarily use that terminology.