SEE-Math

Texas A&M University

Tangrams & Pythagorean Theorem

Manuel, Bollinger

In this activity, the students are first allowed to play with standard tangrams to get the idea of how smaller pieces can be put together to form a larger shape.

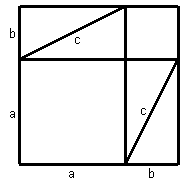
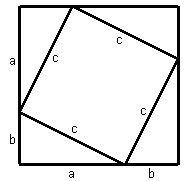
The students are then given 8 right triangles with legs a and b and hypotenuse c, a square of side a, a square of side b and a square of side c.

First, they are asked to use 4 right triangles, the square of side a, and the square of side b to make a square. The solution is shown at the top left. Notice that the square has side a+b.

Second, they are asked to use 4 right triangles and the square of side c to make a square. The solution is shown at the top right. Notice that the square again has side a+b.

Finally, the students are asked to notice that the area of the two solutions are the same. The 4 triangles are then removed from both solutions and the students are asked what they can conclude about the remaining areas. Hopefully, they will conclude that the area of the square of side c must be the same as the sum of the areas of the squares of sides a and b. That is: