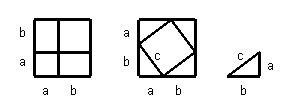




Abstract: With straightedge and compass, the ancient Greek mathematicians (600BC to 400AD) were able to perform many constructions (bisecting any given angle, doubling a square, squaring a given polygon, constructing regular polygons of 3,4,5,6,8 and 10 sides); but they also were unsuccessful in many instances (trisecting any given angle, doubling a cube, squaring a circle, constructing regular polygons of 7 or 9 sides). These problems were some of the most famous unsolved problems in history and the first three of them are frequently called the three unsolved problems of antiquity or the Classical Greek Problems. Why were the Greek mathematicians unable to solve them? Was this merely for lack of ingenuity? Before the end of the 19th century, the impossibility of finding Euclidean constructions for these problems was finally proved, i.e. all of them were proven unsolvable. Why was there a lapse about 2000 years before solutions to the Classical Greek Problems were found?
| Administrative Contacts: | ||
| Jeremy Kubiak | jeremykubiak@tamu.edu | (979) 845-6905 |
| Donna Hoffman | donnalh@tamu.edu | (979) 862-4306 |
| Program Directors: | ||
| Philip B. Yasskin | yasskin@tamu.edu | (979) 574-1697 |
| David Manuel | dmanuel@tamu.edu |
| Senior Counselors: | Junior Counselors: |
| Matthew Barry | Debkonya Banerjee |
| Mitchell Barry | Devkumar Banerjee |
| Mark Cahill | Nicholas Beasley |
| Emma Jakoby | Yaneth Dharmasena |
| Forest Lu | Elia Kim |
| Wolfgang Perez | Malachi Lewis |
| Tommy Settlemyre | Josefina Medina-Perez |
| Kris Watkins | Dominic Motekaitis |
| John Weeks | Navy Singh |
| Bryan Yan; | Logan Tantibanchachai |
| Kevin Yu |

© Philip B. Yasskin, 2002-23.
Last updated June 13, 2023